Você provavelmente assistiu a esse tipo de cena de ficção científica mais de uma vez: algum capitão de nave estrela e sua equipe está fugindo de alienígenas/escapando de uma supernova/ficando sem combustível e estão aparentemente fora de opções, prestes a ser comido/vaporizado/preso. Mas então, logo à frente, eles encontram um planeta! Então eles seguem para isso, foguetes ardentes, depois mergulham e usam sua gravidade para estilingue em segurança. Viva! Cue a música triunfante.
Então, ele vai na tela de prata, pelo menos. Mas essa manobra funciona na vida real?
Sim! Bem, não tanto do jeito que é feito nos filmes – mas é uma coisa real. É amplamente conhecido como um estilingue gravitacional, embora a maioria dos cientistas se refira a ele como uma assistência gravitacional, e é uma ferramenta essencial para a maioria das missões interplanetárias.
Sobre apoiar o jornalismo científico
Se você está gostando deste artigo, considere apoiar nosso jornalismo premiado por assinando. Ao comprar uma assinatura, você está ajudando a garantir o futuro das histórias impactantes sobre as descobertas e idéias que moldam nosso mundo hoje.
A ideia parece bastante simples. À medida que uma espaçonave se aproxima de um objeto enorme, digamos, um planeta, a gravidade do planeta dobra sua trajetória, mudando a direção da espaçonave. Mas há mais do que isso: a espaçonave pode realmente usar a gravidade do planeta para acelerar ou desacelerar após esta manobra, permitindo viagens mais fáceis para os planetas externos ou internos, respectivamente.
Embora a parte da flexão da trajetória pareça óbvia o suficiente, essa parte acelerada ou arborizada é bastante contra-intuitiva. Está relacionado à simetria da gravidade.
Se você segurar uma bola de borracha a alguma distância do chão e soltá -la, a bola acelerará quando cai, acelerando até o impacto. Então ele salta, movendo -se para cima e desacelerando o que faz isso. Eventualmente, ele vai parar, quando você pode pegá -lo ou deixá -lo cair novamente. Mas de qualquer maneira, não pode saltar mais alto do que a altura da qual você o deixou cair. Ganhou energia cinética – a energia do movimento -, como caiu, mas depois a perdeu mais uma vez após o bounce, quando diminuiu o caminho de volta. Essa ação é simétrica, portanto, na melhor das hipóteses (se você tivesse uma bola perfeitamente elástica e fez esse experimento no vácuo), ele saltaria para a mesma altura da qual você a largou.
O mesmo vale para uma espaçonave se aproximando de um planeta. A gravidade do mundo o acelerará quando você cair, você vai se aproximar mais próximo (essa é a parte “slingshot”) e depois perderá essa velocidade extra à medida que se afasta porque a gravidade do planeta ainda está puxando você. À medida que esse aperto gravitacional se afasta, a espaçonave estará se movendo em relação ao planeta na mesma velocidade em que se aproximou inicialmente.
Então, se toda a velocidade de bônus for perdida na saída, como essa manobra pode ser usada para acelerar uma espaçonave? A chave está na frase “em relação ao planeta”. Se você se aproximar do planeta em, digamos, 20 quilômetros por segundo (km/s), sairá com a mesma velocidade. Mas essa é a sua velocidade medida contra o planeta.
Nesse mesmo tempo, crucialmente, o planeta também está orbitando o sol. Se você se aproximar do planeta por trás (isto é, na direção de seu movimento), então, como a gravidade do planeta lhe dá um impulso, também, em um sentido heliocêntrico, o puxa, acrescentando parte de sua velocidade orbital à sua. Isso dá um chute em relação ao sol, acelerando você no seu caminho para o seu destino. Em essência, a espaçonave obtém um ganho líquido de velocidade roubando um pouco da energia cinética orbital do planeta.
Por sua vez, isso significa que o planeta realmente diminui um pouco em sua órbita ao redor do sol – que parece perigoso! Mas não tema: o planeta diminui a proporção de quão mais maciço ele é do que a espaçonave. Dada uma sonda típica de uma tonelada em comparação com um mundo multissextilhão de bilhões de toneladas, o planeta não é de maneira mais lenta. Você pode lançar um milhão de sondas e nunca poder dizer a diferença em sua velocidade orbital. Uma bactéria que se afasta enquanto você está andando teria um efeito muito maior sobre você.
A razão pela qual vale a pena dar ao trabalho de assistência gravitacional é que a espaçonave é lançada por foguetes, que só podem acelerar para alguma velocidade máxima. Para nossa foguetria atual, essas velocidades são tão baixas e as distâncias interplanetárias tão grandes que mesmo as viagens mais rápidas e diretas levam anos (ou mesmo décadas para destinos no sistema solar externo). Você pode carregar a espaçonave com mais combustível para queimar para ir mais rápido, mas também há um limite para isso. O combustível tem massa e você precisaria acelerar essa massa extra, que leva mais combustível, que tem mais massa. Este catch-22 é descrito pelo que é chamado de equação do foguete e significa a quantidade de combustível que você deve adicionar para se mover até um pouco mais rápido, alcance escalas proibitivas muito rapidamente.
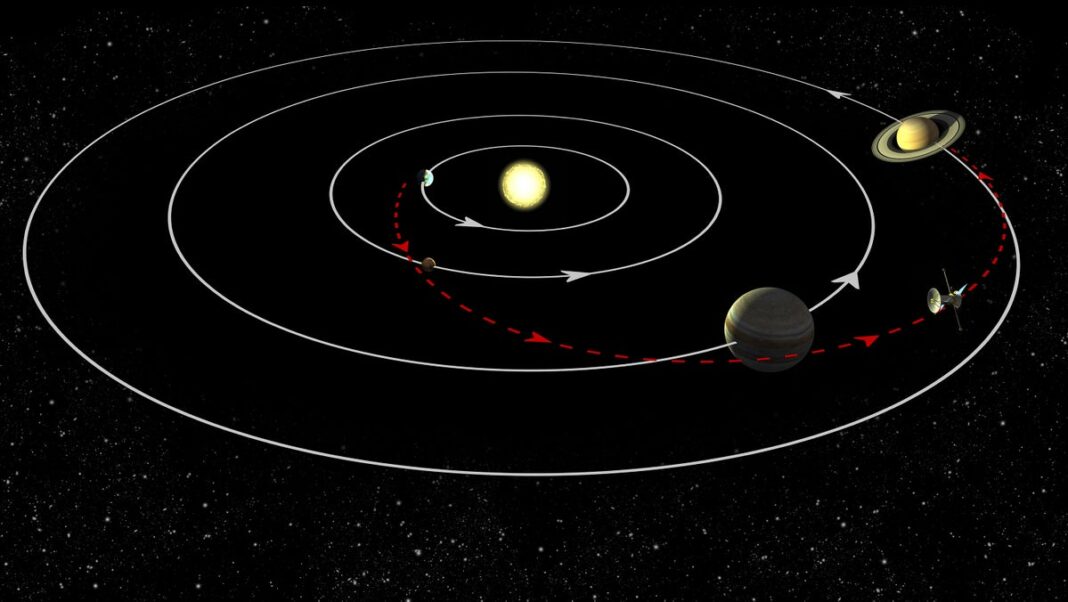
Portanto, o tempo de barbear fora da sua viagem exige algum outro método – como a velocidade de desviação de um grande e suculento planeta ao longo do caminho! Por exemplo, a sonda Cassini para Saturno, lançada em 1997, era uma enorme nave espacial, do tamanho de um ônibus escolar e tinha uma massa de 2,5 toneladas sem combustível. (A adição do combustível necessária para cumprir sua missão em Saturno, juntamente com o veículo de lançamento e outros equipamentos, inclinou a balança a 5,7 toneladas.) Seria necessário praticamente uma eternidade para chegar a Saturno com os foguetes que tínhamos na época. Assim, os planejadores da missão se aproveitaram de Júpiter, enviando a espaçonave passando por uma manobra de estilingue que se move a velocidade que raspava um tempo significativo da jornada. De fato, apenas para sair para Júpiter em primeiro lugar, a Cassini também realizou dois flybys de Vênus e um de Terra, roubando a energia orbital planetária todas as vezes.
Uma assistência gravitacional também funciona de outra maneira. A Terra orbita o sol a mais de 30 km/s, então disparar uma sonda no sol ou nos planetas internos é extremamente difícil por causa de toda essa velocidade lateral. Em vez disso, os planejadores da missão preferem uma rota mais tortuosa. Eles lançam a espaçonave com velocidade suficiente na direção oposta do caminho da Terra ao redor do sol para cair na frente de, digamos, Vênus, onde pode doar parte de sua energia orbital para o planeta cair ainda mais em direção ao sol. Bepicolombo, uma Agência Espacial Européia Conjunta e Missão da Agência de Exploração Aeroespacial do Japão para Mercury, fez exatamente isso, passando pela Terra uma vez e Vênus duas vezes para entrar nas proximidades de Mercury. Mesmo assim, teve que fazer um total de seis A gravidade ajuda além de Mercúrio a combinar com a velocidade orbital do planeta ao redor do sol. A última assistência foi em janeiro de 2025 e entrará em Mercury Orbit em novembro de 2026.
Assistências gravitacionais são um exemplo emblemático de por que a viagem espacial é duro-isto é Afinal, exatamente ciência do foguete. A gravidade é o maior culpado; Apenas fugir da Terra em primeiro lugar é a maior parte do problema. É irônico, então, que a gravidade possa facilitar muito a alcance da maior parte do sistema solar.